Calibration¶

Quantitative AFM starts with a good calibration of the cantilever and ImAFM™ requires this calibration before you start to scan a surface. The AFM Software Suite contains the latest methods for cantilever calibration based on the measurement of the thermal Brownian motion of the cantilever and a theory of hydrodynamic damping of the oscillating beam. By fitting a theoretical model to the noise data we determine all constants necessary to the measure the cantilever deflection in meters, and convert this deflection to force in Newtons.
The IMP Suite determines the parameters of the cantilever as a dynamic transducer of force. ImAFM™, being a dynamic method of force measurement, requires the stiffness of the beam in the frequency band of the measurement (near resonance), which is not the same as the static bending stiffness of the beam. The method works with the fundamental eigenmode of the cantilever, or the resonance with lowest frequency. Details and references to the literature are given in the advanced section on Noise Calibration. Here we describe how to perform the calibration.
The tab at the very top selects between calibration of the Flexural or Torsional eigenmode. The latter calibration is available if you have the Intermodulation Frictional Force Microscopy (ImFFM) option. The calibration procedure is very much the same for either type of mode, but the underlying formulas and analysis are different. We begin by describing calibration of the flexural eigenmode, and end with a discussion of the torsional eigenmode.
Note
For the calibration to be accurate, is important that the calibration is performed when the cantilever is well free of the surface, at least several cantilever widths or about 0.1 mm or more from the surface.
Choose Cantilever and Method¶
Calibration Parameters specifies the type of cantilever and calibration method.
Temp [C]is the temperature of the damping medium which is in thermal equilibrium with the cantilever. This temperature determines the magnitude of the thermal noise fluctuation force that is driving the cantilever.Fluidselects the density and viscosity of the damping medium surrounding the beam, needed for calculation of hydrodynamic damping. Noise calibration methods have not been tested thoroughly beyond studies inAir, but we include to option to apply the theory inWater 20 C.Cantileverselects from a list of cantilevers for which calibration constants have been published. If your cantilever is not on this list you can chooseArbitrary Rectangularand enter the cantileverLength, L [um]andWidth, b [um]of your rectangular beam cantilever. You can edit the length and width fields for any chosen cantilever without changing the stored values for that cantilever. Alternatively, you can Add Edit Remove cantilevers as described below.
Methodselects between six methods of calibration:Hydrodynamic functionuses an analytic expression for the hydrodynamic function to calculate the damping. The calculation applies to a rectangular beam in the limit,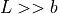 (see [Sader-1998]). This method uses length and width given in the fields above.
(see [Sader-1998]). This method uses length and width given in the fields above.Sader constantsuses a good approximation to the hydrodynamic function described with three parameters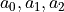 that are specific to the particular type of cantilever. These constants have been measured and checked against other methods and according to theory they should apply to any cantilever of the same shape (see [Sader-2012]). For this method, the length and width fields have no influence.
that are specific to the particular type of cantilever. These constants have been measured and checked against other methods and according to theory they should apply to any cantilever of the same shape (see [Sader-2012]). For this method, the length and width fields have no influence.Reference calibrationbrings up three fields. If you have one good calibration for a particular type of cantilever made with some other means, such that you know all three constants: the quality factor, stiffness and resonant frequency, orQ-ref,k-refandf0-refrespectively, you can use this calibration as a reference for calibrating other cantilevers of the same shape (see [Sader-2012]). For this method, the length and width fields have no influence.Thermal tune: responsivitybrings up a field to enter the known stiffness of the cantilever fundamental eigenmode,k [N/m]. The thermal noise measurement is then applied to determine the detectors inverse responsivity [nm/V].Thermal tune: stiffnessbrings up a field to enter the known detector inverse responsivity,Inv. resp. [nm/V]. The thermal noise measurement is then applied to determine the cantilever mode stiffness.Manualoverrides the thermal noise measurement and no hydrodynamic damping theory is applied. All four calibration constants are entered in the fields given: the eigenmodes resonance frequencyf0 [Hz], dimensionless quality factorQ [-], mode stiffnessk [N/m], and the detectors inverse responsivityInv. resp.[nm/V].
Measure noise¶
Acquire Data controls the start of measurement, saves data, or loads previous measurement data.
Run calibrationstarts the averaging of many separate noise measurements, to decrease the fluctuations in the noise data. If Frequency Sweep was used to find the resonance andTransfer results to noise calibrationwas activated, the software will automatically analyze an appropriate frequency range around the resonance. The Status Banner indicates the progress of the calibration.Settingsopens anAcquisition Settingsdialog box where you can select the total number ofMeasurementsin the average, theCenter frequency [kHz]andFrequency span [kHz]to analyze, and theFrequency resolution [Hz]between data points. You can also give aDown-samplingfactor which averages the given number of samples before transferring to the computer for spectral analysis.Save Asopens a dialog box to save the noise data to a .txt file. IfAutosaveis checked (on the bottom Status Banner of the main frame), calibration files will be automatically saved. The file is saved in the JSON format, and it can easily be opened in many different programing languages (Matlab, Python, Java, etc.) It is not necessary to save the raw noise data for each calibration, as the software automatically keeps track of the Current calibration, or most recent fit of calibration data, which is stored as the relevant calibration in the scan file.Loadopens a dialog box to load a previously saved noise data.
Fitting noise data¶
When the Enable Fit box is checked, the fit is performed in real time and displayed in the plot as a solid blue line. The noise contribution from the cantilever motion is shown with the yellow dash line. For a full description of the theory and fit, see Noise Calibration.
Sometimes very low level spurious signals can be picked up when measuring noise. If the spurious signal is not actually exciting the cantilever (i.e. present on the drive voltage), then you can improve the calibration by simply removing it from the fit. Select the following tools in the calibration plot toolbar:
Calibration Result¶
The Calibration Result is displayed in several ways, including important figures of merit to judge the quality of the calibration. It is useful to think of the calibration as having two parts: The calibration of the cantilever (the force transducer) and the calibration of the detector (the deflection sensor, or optical lever).
Cantilever:
Resonance frequency![f_0 = \sqrt{k/m} \text{ [kHz]}](_images/math/6562cff65a632d6113ad3755f42741faa08b4bfc.png) of the simple harmonic oscillator model used to model the cantilever eigenmode with mode stiffness
of the simple harmonic oscillator model used to model the cantilever eigenmode with mode stiffness 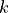 and effective mass
and effective mass 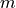 .
.Width of resonance![\gamma \text{ [Hz]}](_images/math/5ee25b57bfdb34d6b40137057edf033e2388c245.png) related to the damping coefficient of the simple harmonic oscillator model.
related to the damping coefficient of the simple harmonic oscillator model. 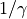 is the characteristic time for exponential decay of oscillation amplitude due to the damping of the surrounding medium.
is the characteristic time for exponential decay of oscillation amplitude due to the damping of the surrounding medium.Quality factor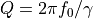 is the ratio of the energy stored in the oscillation, to the energy lost per cycle of oscillation. A freely oscillating cantilever will ‘ring’ for
is the ratio of the energy stored in the oscillation, to the energy lost per cycle of oscillation. A freely oscillating cantilever will ‘ring’ for 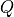 cycles before the amplitude decays by a factor of
cycles before the amplitude decays by a factor of 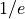 , or 37%.
, or 37%.Mode stiffness![k \text{ [N/m]}](_images/math/c55a50a23eef1f59037dc2b1a0460b85cf63690b.png) is the eigenmode stiffness, or dynamic spring constant, which is the coefficient of the linear restoring force in the simple harmonic oscillator model describing the eigenmode.
is the eigenmode stiffness, or dynamic spring constant, which is the coefficient of the linear restoring force in the simple harmonic oscillator model describing the eigenmode.Thermal noise force![[ \text{ fN/} \sqrt{\text{Hz}} ]](_images/math/21cda93ed4a655d26488fa9ca75d5f8b9f28f8f8.png) is the fluctuation force associated with the linear, viscous damping of the cantilever. This frequency-independent force noise gives rise to a peak in the deflection noise near a high-Q resonance. The thermal noise force represents a fundamental sensitivity limit for force measurement (see Note on sensitivity and accuracy).
is the fluctuation force associated with the linear, viscous damping of the cantilever. This frequency-independent force noise gives rise to a peak in the deflection noise near a high-Q resonance. The thermal noise force represents a fundamental sensitivity limit for force measurement (see Note on sensitivity and accuracy).
Detector:
Inverse responsivity![|\alpha|^{-1} [\mu m/\text{V}]](_images/math/1058d1353332348397fe5e9267292b21d117d2fd.png) is the inverse magnitude of the detectors response function, which converts the measured signal in Volts [V] to a deflection of the tip in meters [m]. In the literature, this constant is often referred to as the ‘inverse optical lever sensitivity’ (invOLS), but we prefer the term ‘responsivity’ (see Note on sensitivity and accuracy for further discussion) . Actually, the calibration internally in the software does not rely on a calibrated measurement of Volts by the MLA™, nor does it rely on the calibration of the AFM scanner to determine detector responsivity. The software uses the noise measurement to determine cantilever deflection in the digital counting units of the MLA™, or Ananog-to-Digital units [ADU]. Thus, the noise measurement and hydrodynamic theory together comprise a more primary form of calibration. All force and distance data given by the AFM Software Suite are derived from this calibration, independent of calibration error in the measurement of detector signal in Volts, or movement of the scanner in nm. The thermal noise method does however depend (weakly) on a calibrated measurement of temperature.
is the inverse magnitude of the detectors response function, which converts the measured signal in Volts [V] to a deflection of the tip in meters [m]. In the literature, this constant is often referred to as the ‘inverse optical lever sensitivity’ (invOLS), but we prefer the term ‘responsivity’ (see Note on sensitivity and accuracy for further discussion) . Actually, the calibration internally in the software does not rely on a calibrated measurement of Volts by the MLA™, nor does it rely on the calibration of the AFM scanner to determine detector responsivity. The software uses the noise measurement to determine cantilever deflection in the digital counting units of the MLA™, or Ananog-to-Digital units [ADU]. Thus, the noise measurement and hydrodynamic theory together comprise a more primary form of calibration. All force and distance data given by the AFM Software Suite are derived from this calibration, independent of calibration error in the measurement of detector signal in Volts, or movement of the scanner in nm. The thermal noise method does however depend (weakly) on a calibrated measurement of temperature.Noise floor![[ \text{fm/} \sqrt{\text{Hz}} ]](_images/math/081fac5117289b15a14210600e4ddb171101541d.png) is the detector noise, expressed as an equivalent deflection noise of the cantilever. The noise floor is a good figure of merit for expressing the sensitivity of the opto-electronic system which detects the cantilever deflection. Note that this noise floor will depend on the type of cantilever (in particular the length) and on the adjustment of the detector (location of laser spot).
is the detector noise, expressed as an equivalent deflection noise of the cantilever. The noise floor is a good figure of merit for expressing the sensitivity of the opto-electronic system which detects the cantilever deflection. Note that this noise floor will depend on the type of cantilever (in particular the length) and on the adjustment of the detector (location of laser spot).Equivalent force![[ \text{fN/} \sqrt{\text{Hz}} ]](_images/math/40c00857fa928529feb29297b56d0521f1d2758c.png) expresses the detector noise as and equivalent force noise acting on the cantilever. This equivalent force noise gives the sensitivity of force measurement, if the same cantilever were to measure force quasi-statically, or at low frequency well below resonance.
expresses the detector noise as and equivalent force noise acting on the cantilever. This equivalent force noise gives the sensitivity of force measurement, if the same cantilever were to measure force quasi-statically, or at low frequency well below resonance.Peak to flat ratio![[\text{dB}]](_images/math/1fb4dd5f61f795b15c4050042e54f0736cf2f4c7.png) is the ratio of the noise peak (thermal noise) to the flat background noise (detector noise). If you compare measurements with the same cantilever and two different detectors, the larger this number, the better the detector (see Note on sensitivity and accuracy).
is the ratio of the noise peak (thermal noise) to the flat background noise (detector noise). If you compare measurements with the same cantilever and two different detectors, the larger this number, the better the detector (see Note on sensitivity and accuracy).
Finally, the Calibration panel shows three plots of Stiffness, Res. freq. and Q-factor which are updated as the data is averaged and re-anlayzed. These plots allow you to judge how many measurements are required to converge to a stable value.
Current calibration¶
Running a new calibration, loading a previous calibration, selecting a new range or excluding points, runs the fitting routine which determines all the calibration constants. These constants define the current calibration. After each scan, all calibration constants from the current calibration are stored with the scan file, together with the raw spectral data acquired by the MLA™. It is not necessary to store a calibration file in order to analyze the data in scan file. The Store and Load features are there only if you want to store or view raw noise data for a particular run of the calibration. The raw noise data and the calibration plot will be saved for each run if Autosave is checked. It is very easy to re-calibrate during a scan session and thereby re-define the current calibration. Simply stop the scan, retract the probe well away from from the surface (at least several cantilever widths, at least 0.1 mm), and re-run the calibration. We recommend that you re-calibrate frequently, to check if anything has changed with the cantilever and detector. Calibration should also be re-run if any adjustments have been made to the laser or the detector, and it must be performed with every new cantilever, before you start to scan with ImAFM™.
Add Edit Remove cantilevers¶
In the Calibration Parameters group, the Cantilever selector has the option to Add / Edit / Remove cantilevers. This option does not change the selected cantilever. It opens a dialog box that allows you to change calibration parameters of the selected cantilever, or create a new cantilever.
The Add tab has two options for creating a new cantilever:
Basicis for rectangular cantilevers. Enter theLength, L [um]andWidth, b [um]in micrometers. Make sure that you enter aCantilever nameand theManufacturer. ClickAddand your cantilever will appear in the pull-down list. The calibration method will will be based on the theoretical expression for the hydrodynamic damping function, valid for(see
Methodabove).
Advancedis for cantilevers of arbitrary plan-view dimensions. Here you can enter theSader Constantsif they are known, or the calibration parameters of aReference calibrationfor a cantilever of the same plan view dimensions (seeMethodabove). Length and Width are interpreted as effective values for a non-rectangular cantilever. TheShapeselector is used to specify that the cantilever is, or is not rectangular.Click
Addto create the new cantilever, which will appear at the bottom of the cantilever selection list with the name user_cantilever-name. Creating a new cantilever does not effect the selected cantilever. Close the dialog box and select the new cantilever.
The Edit tab allows you to change calibration parameters of the selected cantilever.
The Remove tab allows you to remove a user-added cantilever from the selection list.
Calibrating torsional eigenmodes¶
Torsional calibration uses the same principals as flexural calibration, but the methods are not as well tested and established as flexural callibration. We provide two methods for calibrating the lowest torsional eigenmode:
Torsional: Hydrodynamic Functionuses the analytical expression for the hydrodynamic function of a long rectangular beam, calculated by Green and Sader [Green-2002]. This method calibrates the fundamental eigenmode using the length and width values given in the fields above.Torsional: Flexural + beam theoryrequires that you first calibrate the flexural eigenmode. If this is done, the mode stiffnessk_flexand the resonant frequencyf0_flexshould appear in the fields below. This method uses the ratio of resonant frequencies of the torsional and flexural modes, to calibrate the torsional mode in reference to a calibrated flexural mode. The method is explained in a paper by [Thoren-2017] .




