Communicating with the MLA™¶
Working with the MLA GUI is easy and convenient. Data capured in the GUI can be stored to a text file using the save data button  found in many panels. However, to unleash its full power, you need to learn how to program the MLA™ in Python using the MLA API, as described in the section MLA programming. Before getting in to the details of programming, it is useful to understand some basic concepts in working with MLA™ data.
found in many panels. However, to unleash its full power, you need to learn how to program the MLA™ in Python using the MLA API, as described in the section MLA programming. Before getting in to the details of programming, it is useful to understand some basic concepts in working with MLA™ data.
data streams¶
The MLA™ is designed for fast and continuous sampling of a signal. When used with the setup and tuning functions, the signal is optimally sampled for discrete Fourier analysis. Discrete Fourier analysis on the optimally sampled time stream can then be performed on the computer using the Fast Fourier Transform (FFT). The result is the full Fourier spectrum. However, time streams can not go on indefinitely at the full speed of the DAC, as this generates is too much data too fast. Lengthy times streams require down-sampling, or some other form of compression, for example the lockin (Foruier analysis).
The MLA™ lockins perform the Fourier analysis in real-time on the FPGA on a limited number of user-defined frequencies. Immediately after the acquisition of last sample in a measurement time window 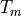 , the MLA™ starts then next lockin calculation, without skipping a single sample. The lockin data is transfered to the computer as a lockin stream, representing a partial spectogram of quadrature amplitudes evolving on a time scale slower than
, the MLA™ starts then next lockin calculation, without skipping a single sample. The lockin data is transfered to the computer as a lockin stream, representing a partial spectogram of quadrature amplitudes evolving on a time scale slower than 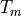 , with no spurious phase jumps.
, with no spurious phase jumps.
The streams of lockin data or time data are buffered in different stages, the first being one Gigabyte memory inside the MLA™. This MLA™ buffer is continuously filling in new data and emptying old data. When the command lockin.Lockin.start_lockin() or osc.Osc.start_time_stream() is issued, an automatic data transfer will begin, sending the data down stream to the computer via Ethernet. The Ethernet receiver runs as a process in the computers operating system which is separated from the rest of the measurement software. This separation ensured that the computer is always ready to receive new data, even when processing or plotting the data is blocking the measurement software.
Below we describe how to work with data streams in general terms. For detailed documentation and additional example scripts, refer to the section on MLA programming and the documentation of the MLA API.
streaming lockin data¶
Lockin data for all tones calculated during one measurement time window forms a unit of data that we call a pixel . This pixel is bunched together with some meta data to form a Lockin data packet. The command lockin.Lockin.start_lockin() starts a stream of lockin data packets to the computer. During this stream, multiple readout commands are issued to extract buffered data and bring it in to Python. The extraction commands are either lockin.Lockin.get_pixels() or lockin.Lockin.get_new_pixels().
This code example waits for one pixel to finish, then gets that pixel.
mla.lockin.start_lockin()
mla.lockin.wait_for_new_pixels(1)
pixels, meta = mla.lockin.get_pixels(1)
mla.lockin.stop_lockin()
Typically the user will have a loop to read data and perform other tasks such as plotting and further processing. While the computer CPU is loaded with these tasks, new measurement data will be buffered for the user to extract in the next iteration of the loop. See the example script lockin measurement loop. Refer to the Python documentation lockin.Lockin for full details.
lockin data formats¶
Multifrequency lockin data is contained in numpy arrays with different formats, depending on how the data is used. Implicit in these formats is the mapping of the array index to a tones in the MLA, which we call the tone index. The mapping between the tone index and the actual frequency of the tone is done with the frequency array:
freqs = np.array([
])
where N is the number of tones in the MLA™.
Note that in this context, 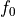 is not the resonance frequency, but the frequency of the tone with index 0.
The frequencies can be expressed in Hz, for example when using
is not the resonance frequency, but the frequency of the tone with index 0.
The frequencies can be expressed in Hz, for example when using lockin.Lockin.set_frequencies().
Before using this function, tuning should be performed (see setup and tuning functions).
Alternatively you can specify the frequencies as an array of integers, which are the multiples of the measurement bandwidth, and use lockin.Lockin.set_frequencies_by_n_and_df().
The response at all measured frequencies, referred to as a pixel of lockin data, are expressed in different ways that are all equivalent and can be transformed to one another. Depending on how this data is used, you will encounter the following formats:
IQ-real¶
An array of real numbers, with the quadrature amplitudes at each tone listed pair-wise.
pixel = np.array([
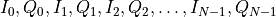 ], dtype=float)
], dtype=float)
This format follows the Lockin data packet.
Note that the array size is 2N, and the index mapping here must step by two in order for the tone index of the 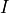 and
and 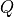 values to coincide with the tone index of the frequency array.
values to coincide with the tone index of the frequency array.
IQ-complex¶
An array of complex numbers, the real part being the amplitude of the 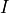 quadrature and the imaginary part the amplitude of the
quadrature and the imaginary part the amplitude of the 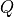 quadrature.
quadrature.
pixel = np.array([
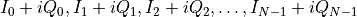 ], dtype=complex)
], dtype=complex)
This format is useful when performing Fourier analysis, as numpy FFT functions will work on complex arrays. Note that the array size is N, so the tone index here does coincide with the tone index of the frequency array.
amp and phase¶
Two arrays of real numbers
pixel_amp = np.array([
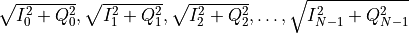 ], dtype=float)
], dtype=float)pixel_phase = np.array([
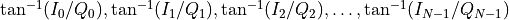 ], dtype=float)
], dtype=float)
Here again the array size is N, so the tone index does coincide with the tone index of the frequency array.
data conversion¶
Depending on what you are doing, different formats may be required. For example when setting drive frequencies, the MLA™ set functions want amplitude and phase as input arguments. Some get functions allow you to get the data in different formats. Whatever the case, it is easy to convert between the different formats using array operations in numpy.
streaming time data¶
Like lockin streams, time streams also need to be started and stopped. However time steams differ in that Python is always blocked until the acquisition is finished. The function osc.Osc.get_data() will wait until the specified number of samples is acquired.
mla.osc.start_time_stream(50000)
mla.osc.get_data(50000)
mla.osc.stop_time_stream()
Time data is currently only available as integer ADU’s. There are several methods for optimally down-sampling the data for faster FFT analysis on the computer. Refer to the Python documentation osc.Osc for more details, or contact Intermodulation Products <info@intermodulation-products.com> if you need further help acquiring time streams.
